Reynolds Number
Osborne Reynolds introduced the Reynolds number (Re) in the late 19th century as a dimensionless quantity used in fluid mechanics to predict flow patterns in various fluid flow situations. This parameter helps determine whether the flow of a fluid, whether liquid or gas, will be laminar or turbulent. The Reynolds number is defined by the following formula:
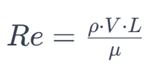
where:
– Re is the Reynolds number.
– ρ is the density of the fluid.
– V is the velocity of the fluid.
– L is a characteristic length (such as the diameter of a pipe or the chord length of an airfoil).
– μ is the dynamic viscosity of the fluid.
Significance of Reynolds Number:
1. Laminar vs. Turbulent Flow:
– A low Reynolds number indicates laminar flow, characterized by smooth, orderly layers of fluid moving parallel to each other.
– A high Reynolds number suggests turbulent flow, characterized by chaotic and irregular fluid motion with eddies and vortices.
2. Critical Reynolds Number:
– There is a critical Reynolds number for each flow situation beyond which the flow transitions from laminar to turbulent.
– The critical Reynolds number depends on factors like the geometry of the flow path and the fluid properties.
3. Flow Stability:
– The Reynolds number is crucial in predicting the stability of flows. For example, flows with low Reynolds numbers tend to be stable and less prone to disturbances.
4. Drag Coefficient:
– In aerodynamics, the Reynolds number is used to predict the drag coefficient of an object moving through a fluid. It helps determine the transition from laminar to turbulent flow over surfaces.
5. Heat Transfer:
– In heat transfer applications, such as in pipes or heat exchangers, the Reynolds number influences the convective heat transfer coefficient.
– The transition from laminar to turbulent flow affects how efficiently heat is transferred.
6. Pipe Flow:
– In fluid flow through pipes, the Reynolds number is crucial for predicting the type of flow. It helps determine whether the flow will be smooth and streamlined (laminar) or chaotic (turbulent).
7. Fluid Mixing:
– In chemical engineering and industrial processes, the Reynolds number is used to predict the efficiency of fluid mixing. High Reynolds numbers often lead to better mixing in certain applications.
8. Modeling and Simulations:
– In computational fluid dynamics (CFD) and fluid flow simulations, the Reynolds number is used to determine the appropriate turbulence models and grid resolutions.
9. Experimental Studies:
– Experimental studies in fluid mechanics often involve changing the Reynolds number to investigate the effects of flow patterns, drag forces, and heat transfer characteristics.
10. Aerodynamic Performance:
– In aerodynamics, the Reynolds number is crucial for predicting the aerodynamic performance of airfoils and wings. It helps determine the lift and drag characteristics.
Understanding the Reynolds number and its significance is fundamental in designing and analyzing fluid flow systems, whether in the context of aerodynamics, heat transfer, or industrial processes. It provides valuable insights into the nature of fluid flow and guides engineers in optimizing designs for efficiency and performance.